

| imho.ws |
 |

|
|
|
# 1 |
|
Junior Member
Регистрация: 05.04.2002
Адрес: Израиль
Сообщения: 93
 |
На вид простое уравнение!
Всем привет!
Уже кучу времени пытаюсь решить следующее уравнение, на вид оно простое, а вот прописного решения ещё ни разу не видел, кто знает, поможите, очень интересно! Само уравнение (точнее система уравнений): x^2 + y = 31 y^2 + x = 41 Само собой ответы я знаю, x=5, y=6. А как решить?
__________________
..:: Deeds Talk Loud Than Words ::.. |
|
|
|
|
# 5 |
|
::VIP::
Регистрация: 19.03.2004
Сообщения: 1 329
    |
Это возвратное уравнение, решается делением обеих частей на y^2, группировкой и заменой y^2+1/y^2 и y+1/y на t^2-2 и t соответственно. Получается простое квадратное уравнение отнсительно t. Ну а дальше просто.
Подробнее: http://matematika.studentu.ru/referats/89170/ Последний раз редактировалось ЕЖ; 01.12.2005 в 17:58. |
|
|
|
|
# 10 |
|
Junior Member
Регистрация: 05.04.2002
Адрес: Израиль
Сообщения: 93
 |
я вот сижу, подставляю, кручу верчу, а нифига не выходит
на ссылке http://www.brsu.brest.by/pages/centr_pmo/au1.html которую дал Madness, описано решение симметричного уравненния четвёртой степени, а в нагем случае это не семметричное уравнение, а головная боль: x^4-62x^2+x+920=0
__________________
..:: Deeds Talk Loud Than Words ::.. |
|
|
|
|
# 11 |
|
Advanced Member
Регистрация: 21.04.2005
Адрес: град Москва
Сообщения: 431
         |
Так. Произвольное уравнение 4-ой степени не решается в общем виде, зря вы голову свою ломаете. Такие уравнения "лечается" теоремой Безу, и, соответственно перебором всех целых делителей свободного члена. В данном случае только так: этим способом можно найти один целый корень. Остальные три - можно попробовать через Формулу Кардано для кубического уравнения: http://algolist.manual.ru/maths/findroot/cubic.php
|
|
|
|
|
# 12 | |
|
Full Member
Регистрация: 19.12.2003
Адрес: Москва
Пол: Male
Сообщения: 514
   |
Цитата:
Школьные методы я уже, разумеется, основательно забыл (лет 7 подобных вещей не решал), единственное, что тут кажется более-менее разумным - это, действительно, подобрать корни из числа делителей (собственно, такой уже есть - 5, как сказано в первом посте), ну а потом кубическое уравнение. С кряхтеньем, но решается. Хотя и не нравится мне жутко этот путь. Должен быть проще. Намного проще...
__________________
Почему же, ё-моё, ты нигде не пишешь "ё"? |
|
|
|
|
|
# 13 |
|
Full Member
Регистрация: 28.02.2003
Адрес: Электричка Москва-Ростов
Сообщения: 578
             |
Есть еще один способ - использовать метод графиков: построить оба и найти точки пересечения

__________________
"Peach, I can eat peach for hours" Faceoff I love this forum!!! "Я возненавидел собственное творение - наконец то я понимаю Бога" Homer Simpson |
|
|
|
|
# 14 | |
|
Advanced Member
Регистрация: 21.04.2005
Адрес: град Москва
Сообщения: 431
         |
Цитата:
PS: Можно получить уравнение (x-y)(x+y-1)=-10 и для него составить восемь простых систем: от {x-y=-1 x+y-1=10} и до {x-y=5 x+y-1=-2}. Решив все системы и подставив в исходное, найдем только целочисленное значения. Иррациональные можно найти через способ выше. |
|
|
|
|
|
# 15 | |
|
Full Member
Регистрация: 19.12.2003
Адрес: Москва
Пол: Male
Сообщения: 514
   |
Цитата:
Просто слишком уж красиво и просто система выглядит... Помнится, мы подобные системы, как семечки щёлкали: это подставить туда, оттуда вычесть то, перекувырнуть через голову, и - оп-ля - биквадратное, или возвратное, или ещё какое-нибудь очень хорошее... Корни, разумеется, иррациональны, и это никакой простоте не противоречит (корень из двух тоже иррационален). Вот только для всех этих кувырков через голову постоянная практика нужна, ибо забывается всё очень быстро.  Можно, конечно, и в самом деле попробовать формулой Кардано... Если кому интересно - вот разложение на множители: x^4 - 62*x^2 + x + 920 = (x - 5) * (x^3 + 5*x^2 - 37*x - 184) Кстати, IncreMan, а в условии точно не было сказано ничего дополнительного? Например, маленькая, незаметненькая фразочка "решить в целых числах" там нигде не запряталась? 
__________________
Почему же, ё-моё, ты нигде не пишешь "ё"? |
|
|
|
|
|
# 16 | ||
|
Advanced Member
Регистрация: 21.04.2005
Адрес: град Москва
Сообщения: 431
         |
Цитата:
 Я сказал нечто другое: то, что вывести это слагаемое простыми методами в данном случае невозможно. Только перебор. Цитата:
|
||
|
|
|
|
# 17 | ||
|
Full Member
Регистрация: 19.12.2003
Адрес: Москва
Пол: Male
Сообщения: 514
   |
Цитата:
 Цитата:
Сейчас погуглил - что-то нашёл по этому поводу: _http://ilib.mirror0.mccme.ru/djvu/encikl/weber-1.htm (это оглавление нехилого djvu-файла)
__________________
Почему же, ё-моё, ты нигде не пишешь "ё"? |
||
|
|
|
|
# 18 | |
|
Advanced Member
Регистрация: 21.04.2005
Адрес: град Москва
Сообщения: 431
         |
Цитата:
|
|
|
|
|
|
# 20 | |
|
::VIP::
Регистрация: 09.09.2002
Адрес: Kiev
Пол: Male
Сообщения: 1 150
               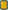 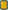 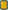 |
Цитата:
 подставляя известный корень в уравнение, находим, что р = -2, т.е. уравнение имеет вид x^2 - 2x - 15 = 0 надеюсь, дальше сама справишься? 
__________________
Great minds discuss ideas. Average minds discuss events. Small minds discuss people. |
|
|
|